Optipedia • SPIE Press books opened for your reference.
Airy Disk
Excerpt from Field Guide to Geometrical Optics
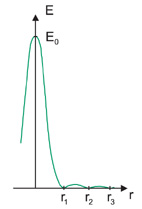
Because of diffraction from the system stop, an aberration-free optical system does not image a point to a point. An Airy disk is produced having a bright central core surrounded by diffraction rings.
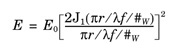
where r is the radial coordinate, J1 is a Bessel function, and f /#W is the imagespace working f /#.
| Radius r | Peak E | Energy in Ring (%) | |
| Central maximum | 0 | 1.0 E0 | 83.9 |
| First zero r1 | 1.22λf⁄#W | 0.0 | |
| First ring | 1.64λf⁄#W | 0.017 E0 | 7.1 |
| Second zero r2 | 2.24λf⁄#W | 0.0 | |
| Second ring | 2.66λf⁄#W | 0.0041 E0 | 2.8 |
| Third zero r3 | 3.24λf⁄#W | 0.0 | |
| Third ring | 3.70λf⁄#W | 0.0016 E0 | 1.5 |
| Fourth zero r4 | 4.24λf⁄#W | 0.0 |
The diameter of the Airy disk (diameter to the first zero) is
D = 2.44λf ⁄#W
| In visible light λ ≈ 0.5 μm and D≈f⁄#W in μm |
The Rayleigh resolution criterion states that two point objects can be resolved if the peak of one falls on the first zero of the other:
Resolution = 1.22λf ⁄#W
The angular resolution is found by dividing by the focal length (or image distance):
Angular resolution=α=1.22λ ⁄ DEP
Citation:
View SPIE terms of use.
J. E. Greivenkamp, Field Guide to Geometrical Optics, SPIE Press, Bellingham, WA (2004).
View SPIE terms of use.
Excerpt from
