Optipedia • SPIE Press books opened for your reference.
Gradient Index Lens
Excerpt from Optical Design Fundamentals for Infrared Systems, Second Edition
Instead of a ball lens, a gradient index lens is frequently used as a fiber coupling element. Such a lens has a gradient profile in which the refractive index varies in the direction perpendicular to the optical axis, as expressed in Eq. (5.23).

where N0 is the base index (at the center of the lens), k is called the Gradient Constant, and r is the variable radius (mm). Figure 1 shows a gradient index rod (GRIN rod) with the length of one full sinusoidal path, or one “pitch.”
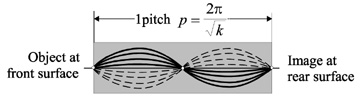
Figure 1 A GRIN rod, one “pitch” long.
Shortening the rod to a length of 1/4 pitch, as shown in Fig. 2, forms a lens with a focal length of


Figure 2 The gradient index lens.
Lenses of that kind are commercially available under the trade name SELFOC, a derivative from “self-focusing.”
If the length of such a lens is identified as t, then the focal length is expressed by1

The back focal length is

Figure 3 shows the details of a GRIN lens with a central index of refraction of N0 = 1.5834 and a gradient constant of k = 0.1067. With a length t = 4 mm, we obtain by using Eqs. (5.25) and (5.26) a focal length of f = 2 mm, and a back focal length of bfl ≈ 0.52 mm.

Figure 3 Details of a GRIN rod lens for an object located at infinity. Such an element is also known as a Wood lens.
Figure 4 shows the same lens as Fig. 3, but now the object is located at a finite distance. To better understand the function of a GRIN lens, an “equivalent” thin lens has been superimposed for reference. This clarifies the object and image distances and, with the fields added, the magnification m=s'/s=h'/h.
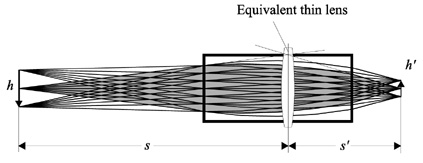
Figure 4 A GRIN lens imaging an object located at a finite distance.
Reference
M. Riedl, Optical Design Fundamentals for Infrared Systems, Second Edition, SPIE Press, Bellingham, WA (2001).
View SPIE terms of use.
Non-Member: $58.00

