Optipedia • SPIE Press books opened for your reference.
Introduction to Optical Pulses
Excerpt from Field Guide to Laser Pulse Generation
An optical pulse is a flash of light. Lasers and related devices have been found to have an amazing potential for generating light pulses with very special properties:
There is a wide range of techniques for generating pulses with durations of nanoseconds, picoseconds, or even femtoseconds with lasers. Such short durations make light pulses very interesting for many applications, such as telecommunications or ultraprecise measurements of various kinds.
Laser pulses are essentially always delivered in the form of a laser beam, that is, they propagate in a well-defined direction. The high spatial coherence of such beams allows the focusing of laser pulses to very small spots, sometimes with areas below 1 µm2. The combination of a small spot size with a short pulse duration leads to very high optical intensities, even if the pulse energy is moderate. The deposition of energy with extremely high concentration in both space and time is essential for applications in material processing, such as micromachining, where ultrashort pulses have the advantage of creating only a very small heat-affected zone around a cut. Other applications are in fundamental sciences, for example, for the study of matter under the influence of extremely high optical intensities.
In some cases, the high temporal coherence within trains of ultrashort pulses is essential. For example, ultraprecise optical clocks exploit this feature.
It is important to note that laser pulses span an enormously large parameter space in terms of pulse duration, pulse energy, and wavelength. This is possible only with a wide range of techniques, the most common of which are discussed in this Field Guide. The following sections, however, focus on basic properties of optical pulses.
Optical Pulses in the Time Domain
In the time domain, a pulse has an optical power P (energy per unit time) that is appreciable only within some short time interval and is close to zero at all other times. The pulse duration τp is often defined as a full width at half maximum (FWHM), that is, the width of the time interval within which the power is at least half the peak power. The pulse shape (power versus time) often has a relatively simple form, described for example with a Gaussian function or a sech2 function, although complicated pulse shapes can occur, for example, as a result of nonlinear and dispersive distortions, when a pulse propagates through some medium.
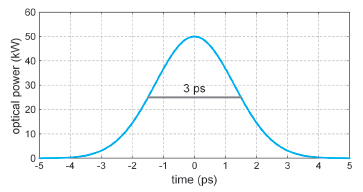
The figure above shows the power versus time for a Gaussian-shaped pulse with 50-kW peak power and a FWHM duration of 3 ps.
Short laser pulses, as generated for example with Q-switched lasers, often have durations in the regime of nanoseconds, while ultrashort pulses from modelocked lasers last only for picoseconds or femtoseconds.
Pulse durations down to a few tens of picoseconds can be measured with fast electronics, while purely optical techniques are required for measuring shorter durations.
The pulse energy Ep is the optical power integrated over time. When the pulse shape is known, the peak power Pp can be calculated from energy and duration according to

where ƒs is a numerical factor depending on the pulse shape. For example, this factor is ≈0.94 for Gaussian-shaped pulses or ≈0.88 for sech2-shaped pulses. In the literature, peak powers are often roughly estimated with the assumption that ƒs is approximately 1.
A pulse is more precisely characterized by its electric field strength E(t), taken at a fixed position, for example, on the beam axis. The field strength is often represented as
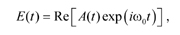
where ω0 = 2πv0 is the central optical angular frequency, and A(t) is a field envelope function, which often exhibits a comparatively slow variation. The optical phase φ is the sum of ω0t and the complex phase of A(t). The envelope function can thus describe both the variation of optical power (or intensity) and a temporal variation of the optical phase.
The temporal derivative of φ, divided by 2π, is the instantaneous frequency
v(t):

If this increases (decreases) with time, the pulse is called up-chirped (down-chirped). Complicated pulses can exhibit a nonmonotonous evolution of frequency. The phase and instantaneous frequency might not even be well defined, for example, when a Q-switched laser emits on multiple resonator modes.
Optical Pulses in the Frequency Domain
Although the time-dependent electric field E(t) contains complete information about a pulse (at least for one location in space), it is instructive also to describe pulses in the frequency domain. The most common description is that based on Fourier spectra, where a Fourier transform is applied to the electric field E(t), resulting in the frequency-dependent Fourier amplitude
E(v). The spectral intensity is the squared modulus of E(v), and the spectral phase is the complex phase of E(v).
Even in cases where the instantaneous frequency v(t) is constant (that is, when the pulse has no chirp), the pulse exhibits a finite spectral width (bandwidth). This is related to physical reality, and not just a mathematical artifact of the Fourier transform. For example, E(v) determines how strongly an atom with a sharp resonance at frequency v can be exited by the pulse. The figure below shows the intensity spectrum for the pulse, with a center frequency of 200 THz and no chirp.
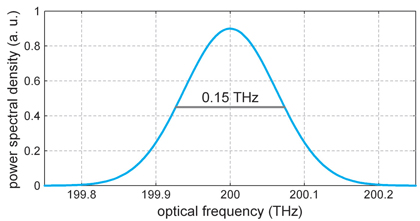
The spectral width is often specified as a FWHM. It can be defined in terms of optical frequency (measured in Hz), angular optical frequency (in rad/s), or wavelength (in nm). The simple formula Δv = Δλ ·(c / λ2) can be used to convert wavelength to frequency bandwidth, if the bandwidth is small.
R. Paschotta, Field Guide to Laser Pulse Generation, SPIE Press, Bellingham, WA (2008).
View SPIE terms of use.

