Optipedia • SPIE Press books opened for your reference.
The Polarization Ellipse
Excerpt from Field Guide to Polarization
According to Fresnel's theory, Ex(z,t) and Ey(z,t) describe sinusoidal oscillations in the x-z and y-z planes, respectively (see the figure on p. 6). By themselves, these equations are not particularly revealing. However, eliminating the time-space propagator ωt - kz between the two equations leads to the equation of an ellipse, namely,
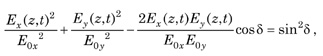
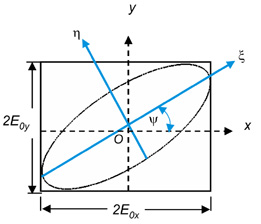
where δ = δy – δx. The above equation describes an ellipse in its nonstandard form. Because the equation refers to polarized light, the equation is called the polarization ellipse. In the equation, the time-space propagator has been explicitly eliminated. Nevertheless, the field components Ex(z,t) and Ey(z,t) continue to be time-space dependent. A plot of the nonstandard polarization ellipse is shown below.
The figure also shows the rotated ξ-η coordinate system. Because of the amplitudes E0x and E0y and the phase δ are constant, the polarization ellipse remains fixed as the polarized beam propagates.
Degenerate Polarization States
In general, the optical field is elliptically polarized, but there are several combinations of amplitude and phase that are especially important. These are called degenerate polarization states: (1) linearly horizontal/vertical polarized light (LHP/LVP), (2) linear ±45° polarized light (L+45P/L–45P), and (3) right/left circularly polarized light (RCP/LCP). The polarization states along with the mathematical conditions and corresponding figures (polarization ellipses) are as follows.
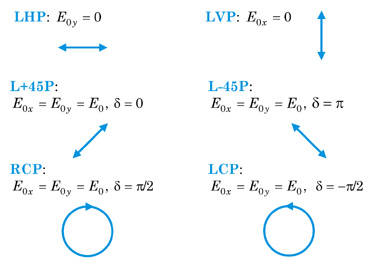
RCP light rotates clockwise and LCP rotates counter-clockwise when propagating toward the observer.
These polarization states are important because (1) they are relatively easy to create in a laboratory using linear and circular polarizers, and (2) polarization measurements as well as many polarization calculations are greatly simplified using these specific polarization states. This is especially true when a polarized beam propagates through numerous polarizing elements.
The Parameters of the Polarization Ellipse
The polarization ellipse can be expressed in terms of two angular parameters: the orientation angle ψ(0≤ψ≤π) and the ellipticity angle χ(–π/4<χ≤π/4).
These angles can be defined in terms of the parameters of the polarization ellipse:
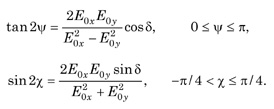
The right-hand side of both of these equations consists of algebraic and trigonometric terms. The two equations can be rewritten completely in trigonometric terms by introducing an angle known as the auxiliary angle α defined by
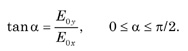
This leads to purely trigonometric equations
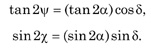
The conditions on the angles are 0≤α≤π/2 and 0≤δ<2π.
| Example: We determine the orientation and the ellipticity angles ψ and χ for RCP light. We have for RCP light that E0y=E0x=E0 and δ=π/2. Then, tan α yields α = 45° and tan2ψ=tan90° cos90°=0 sin2χ=sin90° sin90°=+1 Thus, the angles for RCP light are ψ=0° and χ=+45°. |
E. Collett, Field Guide to Polarization, SPIE Press, Bellingham, WA (2005).
View SPIE terms of use.

